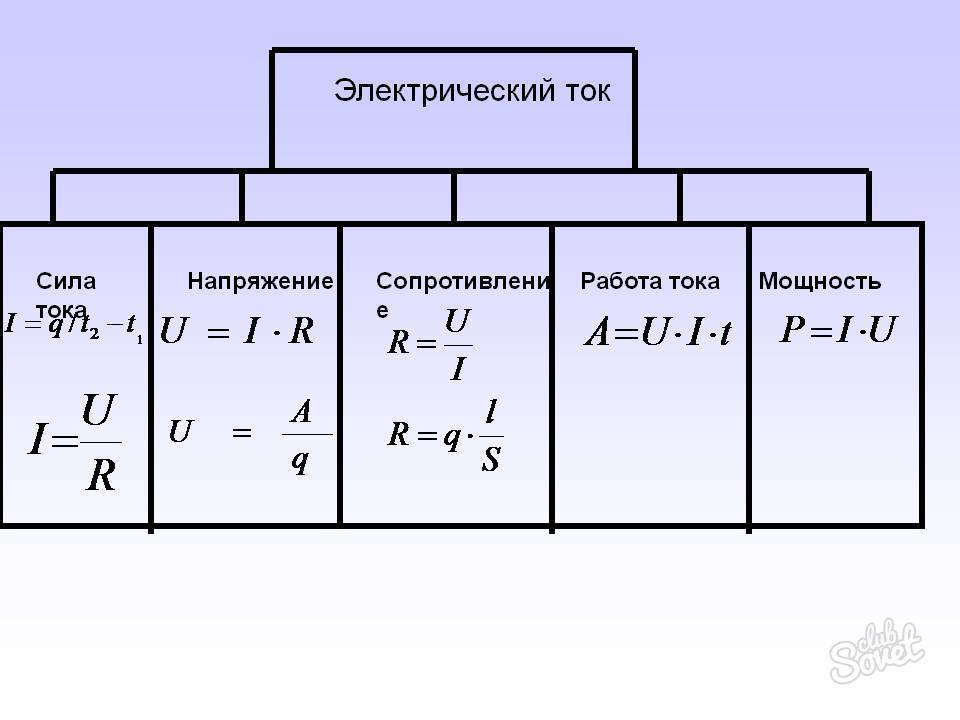
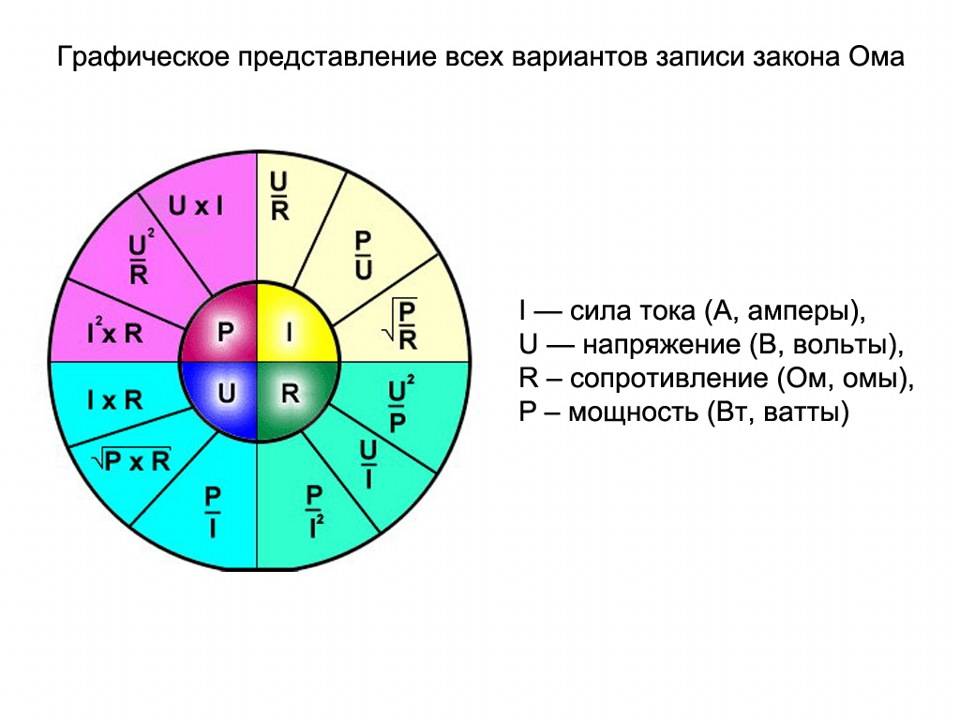
- Beregning for parallel- og serieforbindelse
- Nuværende beregning
- EKSEMPLER PÅ ARBEJDSOPGAVER
- Del 1
- Del 2
- Den samlede effekt og dens bestanddele
- Aktiv belastning
- Kapacitiv belastning
- Induktiv belastning
- Kredsløb og deres varianter
- Egenskaber
- For AC
- 1. Beregning af effektforbrug og strømforløb som en funktion af modstand og anvendt spænding.
- Beregning af kredsløb
- Sådan sparer du penge
- Variation af modstand:
- Brug af formler
- For vekselstrøm
- Spørgsmål om arbejde og effekt af elektrisk strøm
- Interessante oplysninger om emnet
- Wattværdier for vekselstrøm
- Metode til konvertering af kredsløb
- Beregning af et kredsløb med en enkelt strømforsyning
- Beregning af et grenkredsløb med flere forsyningskilder
- Beregning for et enfaset kredsløb
- Konklusion
- Konklusion af lektionen
Beregning for parallel- og serieforbindelse
Når man beregner kredsløbet for en elektronisk enhed, er det ofte nødvendigt at finde den effekt, der frigives på et enkelt element. Derefter skal du bestemme, hvor meget spænding der falder på den, hvis den er forbundet i serie, eller hvor meget strøm der strømmer, hvis den er forbundet parallelt, lad os se på specifikke tilfælde.
Her er I i alt lig med:
I=U/(R1+R2)=12/(10+10)=12/20=0,6
Samlet effekt:
P=UI=12*0,6=7,2 watt
Ved hver modstand R1 og R2 falder spændingen med, da deres modstand er den samme, og spændingen falder med:
U=IR=0,6*10=6 volt
Og er udgivet af:
Pover modstanden=UI=6*0,6=3,6 watt
Så når de er parallelforbundet i et kredsløb som dette:
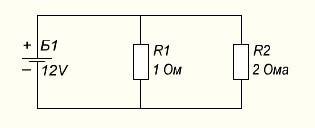
Se først efter I i hver gren:
I1=U/R1=12/1=12 ampere
I2=U/R2=12/2=6 ampere
Og tildelt på hver enkelt:
PR1=12*6=72 Watt
PR2=12*12=144 Watt
Samlet produktion:
P=UI=12*(6+12)=216 watt
Eller via den samlede modstand, så:
Ri alt=(R1*R2)/( R1+R2)=(1*2)/(1+2)=2/3=0,66 Ohm
I=12/0,66=18 ampere
P=12*18=216 Watt
Alle beregninger passede, så de fundne værdier er korrekte.
Beregning af strøm
Værdien af strømmen beregnes på grundlag af effekten og er nødvendig på designstadiet (planlægning) af boligen - lejlighed, hus.
- Værdien af denne værdi afhænger af valget af forsyningskabel (ledning), hvorigennem elektriske apparater kan tilsluttes til netværket.
- Når du kender netspændingen og den samlede belastning af apparaterne, kan du bruge en formel til at beregne den mængde strøm, der skal passere gennem lederen (ledning, kabel). Lederens tværsnitsareal vælges i henhold til dets værdi.
Hvis de elektriske forbrugere i en lejlighed eller et hus er kendt, skal der foretages enkle beregninger for at kunne installere strømforsyningskredsløbet korrekt.
Lignende beregninger udføres til produktionsformål: for at bestemme det nødvendige tværsnitsareal for kabler ved tilslutning af industrielt udstyr (forskellige industrielle elmotorer og maskiner).
EKSEMPLER PÅ OPGAVER
Del 1
1. Strømmen i en leder er blevet forøget med en faktor 2. Hvordan vil den mængde varme, der produceres i en leder pr. tidsenhed, ændre sig, hvis lederens modstand forbliver uændret?
1) øges med en faktor 4
2) med en faktor 2
3) øges med en faktor 2
4) reduceret med en faktor 4
2. Længden af spolen på en elektrisk kogeplade er blevet halveret. Hvordan vil den mængde varme, der produceres i en spole pr. tidsenhed, ændre sig, hvis spændingen forbliver uændret?
1) øges med 4 gange
2) halveret
3) øges med en faktor 2
4) falder med en faktor 4.
3. Modstanden \( R_1 \) er fire gange mindre end modstanden \( R_2 \). Strømmen i modstand 2
1) 4 gange større end modstand 1
2) 16 gange større end modstand 1
3) 4 gange mindre end i modstand 1
4) 16 gange mindre end i modstand 1
4. Modstanden for modstand \( R_1 \) er 3 gange så stor som modstanden for modstand \( R_2 \). Den varmemængde, der vil blive frigivet i modstand 1
1) 3 gange større end i modstand 2
2) 9 gange modstanden 2
3) 3 gange mindre end i modstand 2
4) 9 gange mindre end i modstand 2
5. Et kredsløb er sammensat af en strømkilde, en pære og en tynd jerntråd, der er forbundet i serie. Pæren vil brænde lysere, hvis
1) skift ledningen til en tyndere ledning
2) forkorte længden af ledningen
3) udskift ledningen og pæren
4) udskift jerntråden med en nichromtråd
6. Figuren viser et søjlediagram. Den viser spændingerne i enderne af to ledere (1) og (2) med samme modstand. Sammenlign værdierne af arbejdsstrømmen \( A_1 \) og \( A_2 \) i disse ledere for samme tid.
1) \( A_1=A_2 \)
2) \( A_1=3A_2 \)
3) \( 9A_1=A_2 \)
4) \( 3A_1=A_2 \)
7. Figuren viser et søjlediagram. Den viser strømværdierne i to ledere (1) og (2) med samme modstand. Sammenlign værdierne af strømarbejdet \( A_1 \) og \( A_2 \) i disse ledere for samme tid.
1) \( A_1=A_2 \)
2) \( A_1=3A_2 \)
3) \( 9A_1=A_2 \)
4) \( 3A_1=A_2 \)
8. Hvis en 60 W og 100 W lysekrone bruges til at belyse et rum, så
А. Den højere strømstyrke vil være i 100 watt pæren.
Б. 60 watt-pæren har mere modstand.
Følgende erklæring(er) er korrekt
1) kun A
2) kun B
3) både A og B
4) hverken A eller B
9. Et elektrisk komfur, der er tilsluttet en jævnstrømskilde, bruger 108 kJ energi på 120 sekunder. Hvad er strømmen i kogerens spole, hvis dens modstand er 25 ohm?
1) 36 А
2) 6 А
3) 2,16 А
4) 1,5 А
10. En elektrisk kogeplade bruger 1000 kJ energi ved en strømstyrke på 5 A. Hvor lang tid tager det for strømmen at løbe gennem flisens spole, hvis dens modstand er 20 Ohm?
1) 10000 с
2) 2000 с
3) 10 с
4) 2 с
11. En forniklet spole i en elektrisk komfur blev erstattet af en nichromspole af samme længde og tværsnitsareal. Skab en sammenhæng mellem fysiske størrelser og deres mulige ændringer, når komfuret er tilsluttet. Skriv de valgte tal i tabellen under de tilsvarende bogstaver. Tallene i svaret kan gentages.
FYSISK STØRRELSE
A) elektrisk modstand i en spole
B) elektrisk strøm i spolen
B) elektrisk strøm, der absorberes af komfuret
MØNSTER AF ÆNDRINGER
1) øget
2) nedsat
3) ikke ændret
12. Sammenlign de fysiske størrelser med de formler, hvormed disse størrelser bestemmes. Skriv de tal, du har valgt, under de tilsvarende bogstaver i tabellen.
FYSISKE STØRRELSER
A) nuværende arbejde
B) strømstyrke
B) strømstyrke
FORMULER
1) \( \frac{q}{t} \)
2) \( qU \)
3) \(\frac{RS}{L} \)
4) \( UI \)
5) \(\frac{U}{I} \)
Del 2
13. Et varmelegeme er forbundet i serie med en reostat med en modstand på 7,5 ohm til et kredsløb med en spænding på 220 V. Hvad er varmelegemets modstand, hvis den elektriske effekt i reostaten er 480 W?
Den samlede effekt og dens bestanddele
Elektrisk effekt er en størrelse, der er ansvarlig for ændrings- eller overførselshastigheden af elektrisk effekt. Den er angivet med bogstavet S og er produktet af de effektive værdier af strøm og spænding. Dens måleenhed er volt-ampere (V-A; V-A).
Den samlede effekt kan bestå af to komponenter: aktiv effekt (P) og reaktiv effekt (Q).
Den aktive effekt måles i watt (W; W), den reaktive effekt i watt (Var).
Det afhænger af, hvilken type belastning der indgår i strømforbrugskredsløbet.
Aktiv belastning
Denne type belastning er et element, der yder modstand mod elektrisk strøm. Dette får strømmen til at opvarme belastningen og omdanne elektriciteten til varme. Hvis en modstand af en hvilken som helst modstand er forbundet i serie med et batteri, vil den strøm, der løber i det lukkede kredsløb, opvarme batteriet, indtil det bliver afladet.
Advarsel. Som en aktiv belastning i vekselstrømsnet kan nævnes et eksempel på et elektrisk varmeelement (TEN). Den varme, der genereres på den, er resultatet af elektricitet
Sådanne forbrugere omfatter også pærespiraler, elektriske komfurer, ovne, strygejern og kedler.
Kapacitiv belastning
Kapacitive belastninger er apparater, der kan lagre energi i elektriske felter og kan skabe en strømstrøm fra kilden til belastningen og tilbage igen. Kondensatorer, kabellinjer (kapacitet mellem kerner), kondensatorer i serie- og parallelforbindelse i et kredsløb og induktorer tjener som kapacitive belastninger. Lydforstærkere og synkrone elektriske motorer i overspændingstilstand belaster også linjerne med en kapacitiv komponent.
Induktive belastninger
Når elforbrugeren er bestemt udstyr, herunder:
- transformatorer;
- Trefasede asynkrone motorer, pumper.
På de typeskilte, der er fastgjort til udstyret, er der angivet en karakteristik som f.eks. cos ϕ. Dette er faseforskydningsfaktoren mellem strøm og spænding på det vekselstrømsnet, som udstyret skal tilsluttes. Det kaldes også effektfaktoren; jo tættere cos ϕ er på 1, jo bedre.
Vigtigt: Når en enhed indeholder induktive eller kapacitive komponenter såsom transformere, spoler, viklinger og kondensatorer, halter den sinusformede strøm efter spændingen med en vis vinkel. Ideelt set giver kapacitans en faseforskydning på -900 og induktans en faseforskydning på +900.
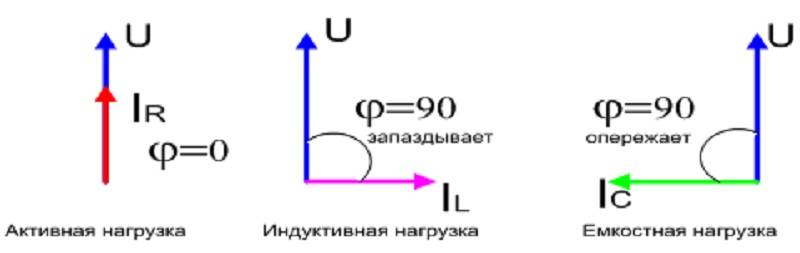 Værdierne for cos ϕ afhænger af belastningstypen
Værdierne for cos ϕ afhænger af belastningstypen
De kapacitive og induktive komponenter danner sammen den reaktive effekt. Formlen for den samlede effekt er således
S = √ (P2 + Q2),
hvor:
- S er den samlede effekt (VA);
- P - aktiv del (W);
- Q - den reaktive del (Var).
Hvis du viser dette grafisk, kan du se, at vektoradditionen af P og Q vil være den samlede værdi af S - hypotenusen i potenstrekanten.
Grafisk forklaring af arten af den samlede effekt
Elektriske kredsløb og deres varianter
Et elektrisk kredsløb er et kompleks af enheder og individuelle genstande, der er forbundet på en bestemt måde. De giver mulighed for passage af elektrisk strøm. En bestemt fysisk størrelse bruges til at beskrive forholdet mellem den ladning, der strømmer gennem hver enkelt leder i et bestemt tidsrum, og varigheden af dette tidsrum. Og det er strømstyrken i et elektrisk kredsløb.
Et sådant kredsløb omfatter en energikilde, energiforbrugere, dvs. en belastning, og ledere. De er opdelt i to varianter:
- Uforgrenet - den strøm, der bevæger sig fra generatoren til energiforbrugeren, ændrer ikke værdi. Det er f.eks. belysning, der kun omfatter én pære.
- Forgrenet - kredsløb, der har nogle forgreninger. Strømmen, der bevæger sig fra kilden, deler sig og går til belastningen langs flere grene. Derved ændres dens værdi.
Et eksempel er belysning, der omfatter en lysekrone med flere arme.
En gren er en eller flere komponenter, der er forbundet i serie. Strømmen strømmer fra knuden med den høje spænding til knuden med den laveste spænding. Den indgående strøm ved knuden er den samme som den udgående strøm.
Kredsløb kan være både ikke-lineære og lineære. Mens førstnævnte har et eller flere elementer, hvor værdierne er afhængige af strøm og spænding, har sidstnævnte ikke en sådan afhængighed. Desuden ændres retningen i kredsløb karakteriseret ved jævnstrøm ikke, mens der i tilfælde af vekselstrøm er en ændring med hensyn til tidsparameteren .
Egenskaber
Vekselstrøm løber gennem et kredsløb og ændrer retning med størrelsen. Den skaber et magnetfelt. Derfor kaldes den ofte for en periodisk sinusformet vekselstrøm. I henhold til loven om kurvelinjen ændrer dens størrelse sig med et bestemt tidsinterval. Det er derfor, den kaldes en sinusoid. Den har sine egne parametre. Af de vigtigste er periode med frekvens, amplitude og øjeblikkelig værdi værd at nævne.
Perioden er det tidsrum, hvor den elektriske strøm ændrer sig og derefter gentager sig igen. Frekvens er strømperiodens varighed pr. sekund. Den måles i hertz, kilohertz og millihertz.
Amplitude - Den aktuelle maksimale værdi med spænding og strømningsvirkningsgrad over en hel periode. Øjeblikkelig værdi - den vekselstrøm eller -spænding, der opstår i løbet af et bestemt tidsrum.
 Karakteristika for vekselstrøm
Karakteristika for vekselstrøm
For vekselstrøm
For et vekselstrømskredsløb er det imidlertid nødvendigt at tage hensyn til den samlede, aktive og reaktive effekt samt effektfaktoren (cosPh). Vi har gennemgået alle disse begreber mere detaljeret i denne artikel.
Det skal blot bemærkes, at for at finde den samlede effekt i et enfaset kredsløb skal strømmen og spændingen ganges med hinanden for at finde den samlede effekt:
S=UI
Resultatet fås i volt-ampere, for at bestemme den aktive effekt (watt) skal S ganges med en koefficient cosPh. Dette kan findes i den tekniske dokumentation for enheden.
P=UIcosF
For at bestemme den reaktive effekt (volt-ampere reaktiv) skal du i stedet for cosF bruge ѕinF.
Q=UIsinF
Eller udtrykke fra dette udtryk:
Og beregn herfra den værdi, du søger.
Det er også nemt at finde effekt i et trefaset netværk ved at bruge formlen til beregning af S (total) ved hjælp af strøm og fasespænding:
S=3Uф/ф
Kendskab til U lineær:
S=1,73*UлIл
1,73 eller roden af 3 - denne værdi bruges til at beregne trefasede kredsløb.
Derefter analogt for at finde P aktiv:
P=3Uф/ф*cof=1,73*UлIл*coSF
Den reaktive effekt kan bestemmes:
Q=3Uф/ф*sinF=1,73*UлIл*sinF
Hermed er de teoretiske oplysninger afsluttet, og vi går over til praksis.
1. Beregner til effekttab og strømforbrug som funktion af modstand og anvendt spænding.
Ohm's lov-demo i realtid.
Til orientering
I dette eksempel kan du øge spændingen og modstanden i kredsløbet. Disse ændringer i realtid ændrer strømmen i kredsløbet og den effekt, der går tabt fra modstanden.
Hvis du ser på lydsystemer, skal du huske, at en forstærker udsender en bestemt spænding til en bestemt belastning (impedans). Forholdet mellem disse to størrelser er afgørende for den afgivne effekt.
En forstærker kan levere en begrænset mængde spænding afhængigt af dens interne strømforsyning og strømkilde. På samme måde er den effekt, som forstærkeren kan levere til en given belastning (f.eks. 4 ohm), nøjagtigt begrænset.
For at få mere effekt kan du tilslutte forstærkeren til en belastning med lavere impedans (f.eks. 2 ohm). Bemærk, at hvis du bruger en belastning med dobbelt så stor modstand (fra 4 ohm til 2 ohm), vil effekten også blive fordoblet (forudsat at den interne strømforsyning og strømkilde kan levere denne effekt).
Hvis vi f.eks. tager en monoforstærker på 100 watt til en belastning på 4 ohm og ved, at den ikke kan levere mere end 20 volt til belastningen.
Hvis du sætter skyderne på vores regnemaskine
Spændingen er 20 volt.
Modstanden er 4 ohm.
Du får
En effekt på 100 watt.
Hvis du flytter modstandsskyderen med 2 ohm, vil du se, at effekten fordobles til 200 watt.
I det generelle eksempel er strømkilden batteriet (ikke forstærkeren), men forholdet mellem strøm, spænding, modstand og impedans er det samme i alle kredsløb.
Beregning af elektriske kredsløb
Alle formler, der bruges til at beregne elektriske kredsløb, er afledt af hinanden.
 Forholdet mellem de elektriske egenskaber
Forholdet mellem de elektriske egenskaber
For eksempel kan effektformlen bruges til at beregne strømstyrken, hvis P og U er kendt.
For at vide, hvor meget strøm et strygejern (1100W), der er tilsluttet et 220V kredsløb, vil trække, skal vi udtrykke strømstyrken ud fra strømformlen:
I = P/U = 1100/220 = 5 A.
Når du kender den beregnede spolemodstand for elkomfuret, kan du finde apparatets P. Effekten gennem modstanden beregnes ved hjælp af formlen:
P = U2/R.
Der findes flere metoder til at beregne de forskellige parametre for et givet kredsløb.
 Beregningsmetoder for elektriske kredsløb
Beregningsmetoder for elektriske kredsløb
Beregning af effekt for kredsløb med forskellige strømstyrker hjælper med at vurdere forsyningslinjernes tilstand korrekt. Husholdnings- og industriapparater, der er udvalgt i henhold til de angivne Pnom- og S-parametre, vil fungere pålideligt og modstå maksimal belastning i årevis.
Sådan sparer du penge
Ved at installere en måler med to takster kan du spare på elvarmeudgifterne. Moskva-taksterne for lejligheder og huse med faste elvarmeenheder skelner mellem to omkostninger:
- 4,65 p fra 7:00 til 23:00.
- 1,26 p fra 23:00 til 7:00.
Så vil du bruge, hvis du antager, at du bruger en 9 kW el-kedel på en tredjedel af dens effekt 24 timer i døgnet:
9*0,3*12*4,65 + 9*0,3*12*1,26 = 150 + 40 = 190 rubler
Forskellen i det daglige forbrug er 80 rubler. På en måned vil du spare 2400 rubler. Dette berettiger installationen af en måler med to takster.
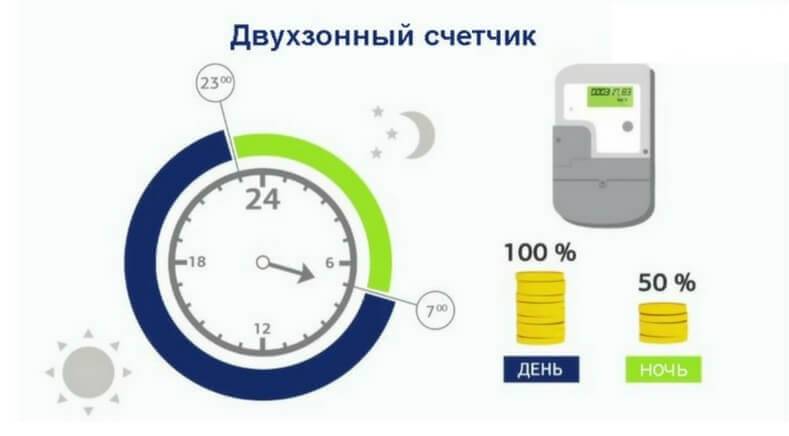
Den anden måde at spare penge på, når du bruger en måler med to takster, er at bruge automatiske apparater til at styre apparaterne. Den består i at placere spidsforbruget af elkedlen, kedlen osv. om natten, så vil det meste af elektriciteten blive opkrævet til 1,26 i stedet for 4,65. Når du er på arbejde, kan kedlen enten lukke helt ned eller køre på et reduceret effektniveau, f.eks. 10 % af kapaciteten. For at automatisere driften af en el-kedel kan du bruge programmerbare digitale termostater eller programmerbare kedler.
Afslutningsvis skal det bemærkes, at opvarmning af huset med elektricitet er ret dyrt, uanset hvilken metode der anvendes, uanset om der er tale om en elkedel, en konvektor eller et andet elvarmeapparat. Det sker kun, hvis der ikke er mulighed for at tilslutte til gas. Ud over driftsomkostningerne til en el-kedel er der de indledende omkostninger ved at sørge for en trefaset elforbindelse.
De største problemer er:
- udarbejdelse af et sæt dokumenter, herunder specifikationer, elprojektdesign osv;
- Anordning af jording;
- udgifter til kabel til hustilslutning og ny kabelføring;
- installation af en måler.
Desuden kan du blive nægtet en trefaset tilslutning og øget kapacitet, hvis der ikke er en sådan teknisk mulighed i dit område, når TS'en allerede arbejder på grænsen af sin kapacitet. Hvilken type kedel og opvarmning du vælger, afhænger ikke kun af, hvad du ønsker, men også af, hvad infrastrukturen kan gøre.
Hermed er vores korte artikel afsluttet. Vi håber, at du nu forstår, hvad det reelle energiforbrug for en el-kedel er, og hvordan du kan reducere omkostningerne ved at opvarme dit hjem med elektricitet.
Antal blokke: 18 | Samlet antal tegn: 24761
Antal anvendte donorer: 7
Oplysninger om hver enkelt donor:
Modstandsændringer:
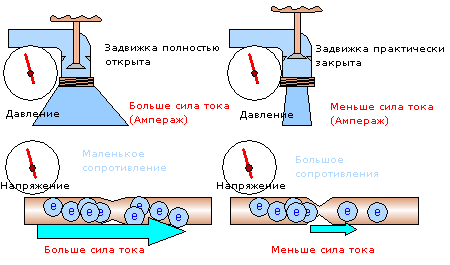
I det følgende diagram kan du se forskellen i modstand mellem de systemer, der er vist i højre og venstre side af figuren. Modstanden mod vandtrykket i vandhanen modvirkes af porten, og modstanden ændres afhængigt af, hvor meget ventilen åbnes.
Modstanden i lederen er vist som en indsnævring af lederen, og jo smallere lederen er, jo mere modvirker den strømgennemgangen.
Du vil bemærke, at spændingen og vandtrykket er det samme i højre og venstre side af diagrammet.
Du skal være opmærksom på det vigtigste faktum. Afhængigt af modstanden øges og mindskes strømmen
Strømstyrken stiger og falder som en funktion af modstanden.
Til venstre ses den største vandgennemstrømning, når spjældet er helt åbent. Og ved den laveste modstand ser vi den største strøm af elektroner (strømstyrke) i lederen.
Til højre er porten lukket meget mere, og vandgennemstrømningen er også meget større.
Lederens modstand er også halveret, hvilket betyder, at modstanden mod strømgennemstrømningen er fordoblet. Som vi kan se, strømmer halvt så mange elektroner gennem lederen på grund af den høje modstand.
Til orientering
Bemærk, at den indsnævring af lederen, der er vist i diagrammet, kun bruges som et eksempel på modstand mod strømgennemstrømning. I det virkelige liv har indsnævringen af lederen kun ringe indflydelse på strømmen
Halvledere og dielektriske stoffer kan yde en langt større modstand.
Indsnævringslederen i skemaet er kun vist som et eksempel for at forstå processens karakter.
I = E/R
Som du kan se af formlen, er strømmen omvendt proportional med kredsløbets modstand.
Mere modstand = mindre strøm
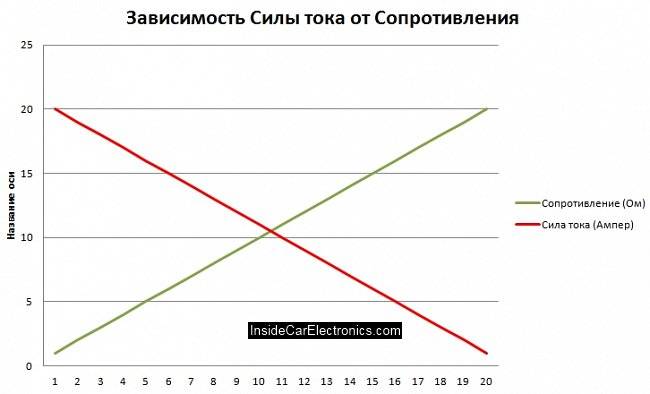
En højere modstand er lig med en lavere strøm *, så længe spændingen er konstant.
Brug formlerne
Denne vinkel er det, der karakteriserer faseforskydningen i et vekselstrømskredsløb, der indeholder induktive og kapacitive elementer. Til beregning af de aktive og reaktive komponenter anvendes de trigonometriske funktioner, der anvendes i formlerne. Før resultatet kan beregnes ved hjælp af disse formler, skal sin φ og cos φ bestemmes ved hjælp af regnemaskiner eller Bradis-tabeller. Herefter anvendes formlerne
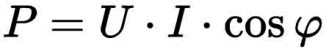
Jeg vil beregne den nødvendige parameter for det elektriske kredsløb. Det skal dog tages i betragtning, at hver af de parametre, der beregnes i henhold til disse formler, på grund af U, som konstant ændrer sig i henhold til lovene for harmoniske svingninger, kan antage enten den øjeblikkelige værdi eller rms-værdien eller en mellemliggende værdi. De tre ovenstående formler er gyldige for RMS-værdier af elektrisk strøm og U. Hver af de to andre værdier er resultatet af en beregningsprocedure med en anden formel, som tager hensyn til tidsforløbet t:
Men det er ikke alle nuancer. For eksempel anvendes formler, der involverer bølgeprocesser, på højspændingsledninger. Og de ser anderledes ud. Men det er en helt anden historie...
For vekselstrøm
For et vekselstrømskredsløb skal du imidlertid tage hensyn til den samlede, aktive og reaktive effekt samt effektfaktoren (cosPh). Vi har set nærmere på alle disse begreber i denne artikel
Lad os blot bemærke, at for at finde den samlede effekt i et enfaset netværk ved hjælp af strøm og spænding skal du gange dem:
S=UI
Resultatet vil være i volt-ampere, og for at finde den aktive effekt (watt) skal du gange S med koefficienten cosPhi. Du kan finde dette i den tekniske dokumentation for enheden.
P=UIcosF
For at bestemme den reaktive effekt (reaktive volt-ampere) skal du bruge ѕinF i stedet for cosF.
Q=UIsinF
Eller udtrykke fra dette udtryk:
Og beregn herfra den værdi, du søger.
Det er også nemt at finde effekten i et trefaset netværk ved at bruge formlen til beregning af S (total) ved hjælp af strøm og fasespænding:
Og kendskab til U-lineær:
1,73 eller roden af 3 - denne værdi bruges til at beregne trefasede kredsløb.
Derefter analogt for at finde P aktiv:
Den reaktive effekt kan bestemmes:
Hermed er de teoretiske oplysninger afsluttet, og vi går over til praksis.
Spørgsmål om elektricitetens arbejde og kraft
Teoretiske spørgsmål om arbejde og effekt af elektrisk strøm kan være som følger:
- Hvad er den fysiske størrelse af arbejdet med elektrisk strøm? (Svaret findes i vores artikel ovenfor).
- Hvad er den elektriske strøms styrke? (Svar givet ovenfor).
- Giv en definition af Joule-Lenz-loven. Svar: Arbejdet fra en elektrisk strøm, der løber gennem en fast leder med en modstand R, omdannes til varme i lederen.
- I hvad måles strømmenes arbejde? (Svar ovenfor).
- Hvad måles magt i? (Svar ovenfor).
Dette er en liste med eksempler på spørgsmål. Essensen af teoretiske spørgsmål i fysik er altid den samme: at kontrollere forståelsen af fysiske processer, forholdet mellem en størrelse og en anden, viden om formler og måleenheder, der er vedtaget i det internationale system SI.
Interessante fakta om emnet
Trefasede strømkredsløb anvendes i produktionen. Den samlede spænding i et sådant net er 380 V. Sådanne ledninger installeres også i etagebygninger og fordeles derefter til lejlighederne. Men der er en nuance, som påvirker den endelige spænding i netværket - tilslutning af kerner under spænding som følge heraf giver 220 V. Trefaset giver i modsætning til enfaset ikke forvrængning ved tilslutning af strømforsyningsudstyr, da belastningen er fordelt i centralen. Men en trefaset forbindelse til et privat hus kræver en særlig tilladelse, så det er almindeligt med en to-leders installation, hvoraf den ene er neutral.
Standarder for vekselstrømsnettet
Spænding og strøm er noget, som alle, der bor i en lejlighed eller i et privat hus, skal vide. Den almindelige vekselstrømsspænding i en lejlighed eller et privat hjem udtrykkes som et tal på 220 og 380 watt. For at kvantificere styrken af den elektriske energi er det nødvendigt at tilføje den elektriske strøm til spændingen eller at måle den nødvendige værdi med et wattmeter. For at måle med wattmeteret skal du bruge styli og særlige programmer.
 Hvad er vekselstrøm
Hvad er vekselstrøm
Vekselstrømmen er defineret som forholdet mellem den mængde strøm og den mængde tid, der produceres i et bestemt tidsrum. Gennemsnitsbrugeren bruger det antal watt, som han/hun har fået af sin elleverandør. Den er normalt på 5 til 12 kilowatt. Disse tal er tilstrækkelige til at sikre, at det nødvendige elektriske udstyr til husholdningsbrug fungerer.
Dette tal afhænger af de eksterne betingelser for strømforsyningen til huset, de strømbegrænsende anordninger (automatiske eller halvautomatiske), der regulerer timingen af strømkapaciteten til forbrugerens strømkilde. Dette sker på forskellige niveauer, fra husstandens eltavle til den centrale elfordelingsenhed.
Kapacitetsbestemmelser i vekselstrømsnettet
Metoden til kredsløbsomdannelse
Hvordan kan jeg bestemme strømstyrken for de enkelte kredsløb i komplekse kredsløb? Det er ikke altid nødvendigt at specificere de elektriske værdier for hver enkelt komponent for at løse praktiske problemer. Der anvendes omregningsmetoder for at forenkle beregningerne.
Beregning af et kredsløb med en enkelt strømforsyning
I en serieforbindelse lægges de elektriske modstande, der er omtalt i eksemplet, sammen:
Rack = R1 + R2 + ... + Rn.
Strømmen i kredsløbet er den samme i alle punkter i kredsløbet. Det kan kontrolleres ved afbrydelsen i testsektionen med et multimeter. Hvert enkelt element (med forskellige værdier) vil dog vise en anden spænding. I henhold til den anden Kirchhoff's lov er det muligt at tydeliggøre resultatet af beregningen:
E = Ur1 + Ur2 + Urn.
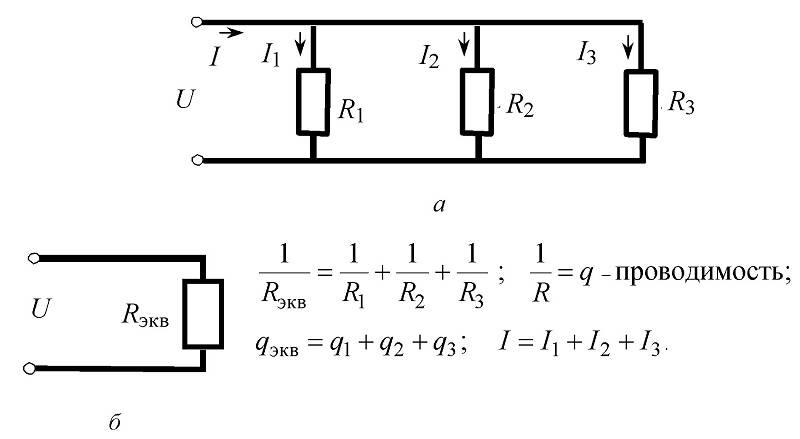 Parallelforbindelse af modstande, kredsløb og formler til beregningerne
Parallelforbindelse af modstande, kredsløb og formler til beregningerne
I denne version er strømmene i fuld overensstemmelse med Kirchhoffs første postulat adskilt og forbundet ved ind- og udgangsknuderne. Den retning, der er vist i kredsløbet, er baseret på polariteten af det tilsluttede batteri. I henhold til de ovenfor beskrevne principper bibeholdes den grundlæggende bestemmelse af ligheden af spændinger på de enkelte kredsløbskomponenter.
Følgende eksempel viser, hvordan man finder strømmen i de enkelte grene. Følgende startværdier anvendes til beregningen:
- R1 = 10 ohm;
- R2 = 20 Ohm;
- R3 = 15 Ohm;
- U = 12 V.
Følgende algoritme anvendes til at bestemme kredsløbets egenskaber:
den grundlæggende formel for de tre elementer:
Rcomm = R1*R2*R3/(R1*R2 + R2*R3 + R1*R3.
- Ved at erstatte dataene beregnes Robsc = 10 * 20 * 15 / (10 * 20 + 20 * 15 + 10 * 15) = 3000 / (200 + 300 + 150) = 4,615 Ohm;
- I = 12/ 4,615 ≈ 2,6 A;
- I1 = 12/ 10 = 1,2 A;
- I2 = 12/20 = 0,6A;
- I3 = 12/15 = 0,8 A.
Som i det foregående eksempel anbefales det, at resultatet af beregningerne kontrolleres. Hvis komponenterne er parallelforbundet, skal ligheden mellem indgangsstrømmene og den samlede værdi overholdes:
I = 1,2 + 0,6 + 0,6 + 0,8 = 2,6A.
Hvis der anvendes et sinusformet kildesignal, bliver beregningerne mere komplicerede. Hvis en transformator er tilsluttet en 220 V enfaset stikkontakt, skal der tages højde for tab (lækage) i tomgangsdrift. I dette tilfælde er viklingernes induktive egenskaber og koblingsfaktoren (transformationsfaktoren) af afgørende betydning. Den elektriske modstand (XL) afhænger af følgende parametre:
- signalfrekvens (f);
- induktansen (L).
XL beregnes efter følgende formel:
XL = 2π * f * L.
For at finde modstanden for en kapacitiv belastning passer udtrykket:
Xc = 1/ 2π * f * C.
Husk på, at i kredsløb med reaktive komponenter er strøm- og spændingsfaserne forskudt.
Beregning af et forgrenet multi-energikredsløb
Ovennævnte principper anvendes til at beregne egenskaberne for komplekse kredsløb. Følgende viser, hvordan man finder strømmen i et kredsløb med to kilder:
- at udpege komponenter og grundlæggende parametre i alle kredsløb;
- Lav ligninger for de enkelte knudepunkter: a) I1-I2-I3=0, b) I2-I4+I5=0, c) I4-I5+I6=0;
- I henhold til Kirchhoffs andet postulat kan vi skrive følgende udtryk for kredsløbene: I) E1=R1 (R01+R1)+I3*R3, II) 0=I2*R2+I4*R4+I6*R7+I3*R3, III) -E2=I5*(R02+R5+R6)-I4*R4
- check: d) I3+I6-I1=0, E1-E2=I1*(r01+R1)+I2*R2-I5*(R02+R5+R5+R6)+I6*R7.
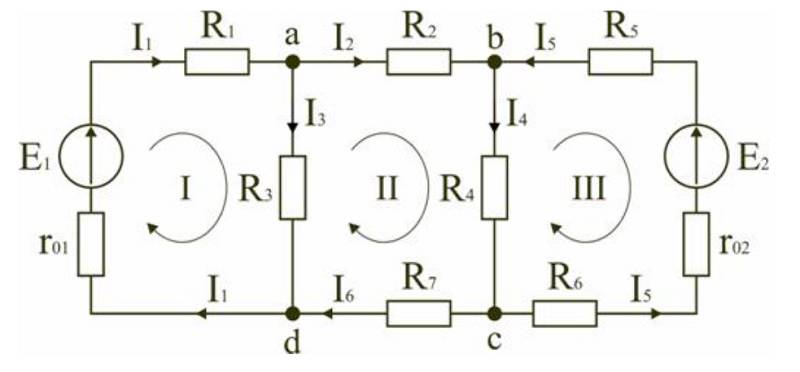 Forklarende diagram for beregning af dobbeltkilde
Forklarende diagram for beregning af dobbeltkilde
Beregning af strøm for et enfaset net
Strømmen måles i ampere. Til beregning af effekt og spænding anvendes formlen I = P/U, hvor P er effekten eller den samlede elektriske belastning, målt i watt. Denne parameter skal registreres på apparatets datablad. U er spændingen i det net, der skal beregnes, målt i volt.
Forholdet mellem strøm og spænding fremgår tydeligt af tabellen:
| Elektriske apparater og elektrisk udstyr | Effektforbrug (kW) | Strømstyrke (A) |
| Vaskemaskiner | 2,0 – 2,5 | 9,0 – 11,4 |
| Elektriske komfurer | 4,5 – 8,5 | 20,5 – 38,6 |
| Mikrobølgeovne | 0,9 – 1,3 | 4,1 – 5,9 |
| Vaskemaskiner | 2,0 – 2,5 | 9,0 – 11,4 |
| Køleskabe, frysere | 0,14 – 0,3 | 0,6 – 1,4 |
| Elektrisk gulvvarme | 0,8 – 1,4 | 3,6 – 6,4 |
| Elektrisk kødhakkemaskine | 1,1 – 1,2 | 5,0 – 5,5 |
| Elektrisk kedel | 1,8 – 2,0 | 8,4 – 9,0 |
Forholdet mellem effekt og strøm gør det således muligt at foretage et foreløbigt skøn over belastningerne i det enfasede net. Størrelsestabellen kan bruges til at hjælpe dig med at vælge den korrekte trådstørrelse afhængigt af parametrene.
| Lederkernediameter (mm) | Tværsnit af ledere (mm2) | Kobberledere | Aluminiumledere | ||
| Strømstyrke (A) | Effekt (kW) | Effekt (A) | Effekt (kW) | ||
| 0,8 | 0,5 | 6 | 1,3 | ||
| 0,98 | 0,75 | 10 | 2,2 | ||
| 1,13 | 1,0 | 14 | 3,1 | ||
| 1,38 | 1,5 | 15 | 3,3 | 10 | 2,2 |
| 1,6 | 2,0 | 19 | 4,2 | 14 | 3,1 |
| 1,78 | 2,5 | 21 | 4.6 | 16 | 3,5 |
| 2,26 | 4,0 | 27 | 5,9 | 21 | 4,6 |
| 2,76 | 6,0 | 34 | 7,5 | 26 | 5,7 |
| 3,57 | 10,0 | 50 | 11,0 | 38 | 8,4 |
| 4,51 | 16,0 | 80 | 17,6 | 55 | 12,1 |
| 5,64 | 25,0 | 100 | 22,0 | 65 | 14,3 |
Konklusion
Som du kan se, er det ikke særlig svært at finde effekten i et kredsløb eller en kredsløbsdel, uanset om der er tale om jævnstrøm eller vekselstrøm. Det er vigtigere at bestemme den samlede modstand, strøm og spænding korrekt.
Denne viden er også nyttig til at bestemme et kredsløbs effekt og til at vælge de rette elementer såsom modstande, kabler og transformatorstørrelser. Du skal også være forsigtig, når du beregner den fulde S-værdi for at kunne beregne rodfaktoren. Det er værd at tilføje, at når vi betaler vores regninger for forsyningsvirksomheder, betaler vi i kilowatttimer eller kWh, som er lig med den mængde strøm, der forbruges i løbet af en periode. Hvis du f.eks. tilslutter et 2 kW-varmelegeme i en halv time, vil måleren opkræve 1 kWh og 2 kWh i en time osv. på samme måde.
Endelig anbefaler vi, at du ser en nyttig video om emnet i artiklen:
Læs også:
- Sådan beregner du apparaters strømforbrug
- Hvordan man beregner kabeltværsnit
- Mærkning af modstande efter effekt og modstand
Resumé af lektionen
I denne lektion har vi kigget på forskellige problemer om blandet modstand af ledere og om beregning af elektriske kredsløb.